Plasticity models; why Femdesigner uses only EPP
This post deals with metals which exhibit an elastic (stress proportional to strain) phase up to a yield point. Hyperelasticity, viscoelasticity as used for rubber or plastics are not included because it is a little more complicated to use such models than we would prefer and results can be wildly wrong. I recommend the polymerfem.com blog for more information on that subject. It also deals with pressure vessel (PV) design codes because that is my specialty. Often a component does not have a design code in which case you can do worse than use a PV code. Code has many meanings: Here it will mean 'design code' but forgive me if I use the same word for FEA software.
In other FE software such as Ansys or Abaqus you can select strain-hardening models. This may seem an advantage but often it isn't; which will be explained if you read on. ASME and EN13445 codes still recommend the use of the Elastic-Perfectly-Plastic model (EPP) with a safety factor (SF) that is roughly 1.5 (though EN13445 splits this between material and load SFs). EN13445 goes even safer than ASME and states that the yield strength should be reduced by 15% to allow for the difference between Tresca (safer) and von-Mises (more accurate on average) yield criteria. By the way, von-Mises yield criterion and flow rule is used for all numerical plasticity analyses because it has no sharp corners, so is easier for numerical computations, while Tresca is used for most hand calculations because it is safer and simpler.
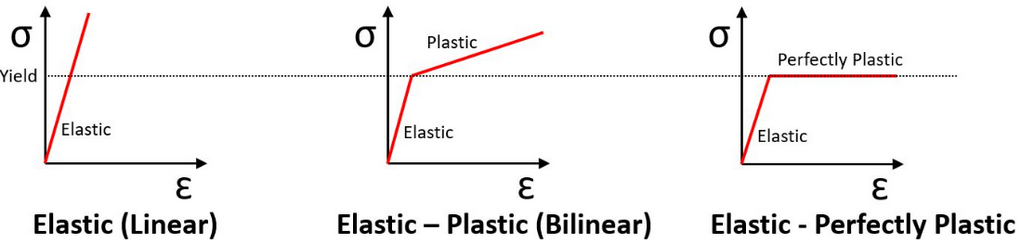
If you really want to add strain-hardening then the safety factor goes above 2 in both codes. Hence the perceived benefit gained from using strain-hardening is entirely lost due to the higher safety factor. The simple reason for this is that code commitee members are aware that extensive physical testing has shown that most material models for inelasticity just plain suck. Worse than that they are almost all unconservative. The author has reviewed the literature extensively to verify this. It is basically a tricky problem that has yet to be adequately solved by even the smartest academics. So EPP is chosen as a conservative approach. Alas the software vendors do not tell you that. They want to sell more product so they include a lot of extra stuff to convince you to select their product over other similar products. Then the other vendors have to play catch-up.
The unique material model yet found by researchers to be uniformly conservative is the Chaboche model. However it is doubtful anyone outside of academia or the author have even used it because there are no code-defined plasticity parameters for this model: You have to search the literature or do your own testing. Moreover it seems to be just a curve-fitting exercise where 15 parameters have to be derived from a single curve obtained from a single cyclic test at a specified temperature for a uniaxial test specimen. Finding these parameters is quite a task, subject to some subjective decisions and optimisation-based solving. Some other papers say there are better models than Chaboche but they always need even more parameters to be derived from the same curve.
So most engineers will use kinematic multi-linear hardening. The kinematic part means that it takes account of the Bauschinger effect whereby the compressive yield point decreases (becomes less negative) while the tensile yield stress increases so that the difference between these points remains at a value of twice yield.
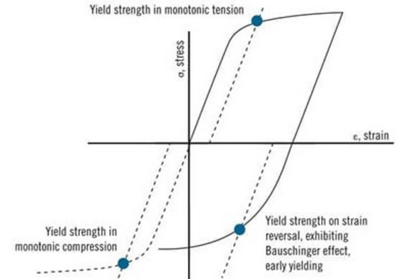
The clear conclusion to reach is that for plastic cycling there is no benefit to including hardening because the shakedown limit remains at twice yield. The argument against that would be that the final strain is more accurate. However it isn't. Moreover residual stresses must be ignored anyway from the outset which is somewhat unrealistic so 'accurate' is a relative concept. There is also a downside to standard kinematic hardening; ratchetting cannot occur and so it is not conservative or even useful. Conversely I have not yet managed to avoid ratchetting using Chaboche which makes it equally useless.
Abaqus claim that a combination of isotropic and kinematic hardening with an extra called 'back-stress' can allow reasonably accurate ratchetting for a uniaxial test specimen. For this you need at least 4 plasticity parameters; Q, b for the isotropic part and C, Y for the kinematic part but it works better with more C, Y pairs. It is unclear where these parameters may be derived from but it's likely to involve curve-fitting and certainly not from any design codes. It seems like thin gruel to me.
Until there is a parameter-friendly plasticity model with minimal, well-defined plasticity parameters, which is sufficiently accurate, or at least conservative, and can predict both shakedown and ratchetting Femdesigner will be sticking to the Elastic-Perfectly-Plastic model - because it just works. If using other FE software you can obtain this setting by setting the tangent modulus to zero (or 1 if that causes trouble). Isotropic and kinematic hardening are the same thing when there is no tangent modulus and hence no Bauschinger effect. The unique occasion when multilinear hardening is useful may be for monotonic loading for a part that has already been damaged. However you may ask yourself, if it is no good for cyclic loading how good can it be really for monotonic loading? Plus remember that higher Safety Factor.
Now you may well also ask, with your new-found knowledge about the suckiness of plasticity material models, what about inelastic buckling analysis accuracy? Well indeed! Fortunately you don't have to use that method (see previous post) and you probably shouldn't unless for something where nobody is likely to die if it fails. Such things aren't encouraged in Femdesigner.
It is perhaps now becoming clear that just because an FEA vendor includes an element or analysis type doesn't mean that it is actually safe to use. It only means they are bulking up their product to be more appealing to those who usually don't know any better.
