Things said about FEA that just aren't true 3
I have only recently noticed the following myth but it seems to be all over the intenet. Modified on 21/8/23 to add myth 2 and ASME VIII division 2 rules.

Reality: For most practical situations that effect is too small to be relevant.
It is true that there will be a slight reduction (say 15% for shells) in buckling prediction but that is dwarfed by the much larger detrimental effect of initial shape imperfections introduced during manufacture; eg out of roundness. For the vast majority of situations an engineer wants to prevent buckling of a slender column, web, flange or thin shell and an Eigenvector buckling analysis when used with a sensible safety factor (usually 2.5) will give you a pass or fail which will ensure your structure will not suffer buckling even if slightly out of shape (ie within code rules) after manufacture. The safety factor was introduced by ASME and is based on empirical measurements of a variety of shapes with imperfections. It is also well proven by use!
Myth 2
We can guess an initial imperfection as a starting point for a nonlinear analysis and the most popular method for doing that is via a prior Euler analysis.
Reality
Using the buckling mode shape remains a guess which may be conservative or unconservative but it cannot ever be considered realistic: Nobody can predict a manufacturing defect! It seems some engineers are content to lose sight of that important point. However, the codes don't; nonlinear buckling analysis also needs a safety factor. This type of analysis is useful in academia but not in the real world where guesswork can kill.
There are several other problems with nonlinear buckling analysis, such as...
a) Not every engineer is capable to appreciate the sensitivities involved in nonlinear analysis; ie the capacity to get a wrong answer and not recognise that it is wrong or how to fix it.
b) Non-linearity can be geometric, plasticity, hyperelasticity, viscoplasticity, etc. At the very least they should say which one is meant.**
c) In fact the most likely scenario is that a crack will appear at a fold and that cannot yet be predicted by FEA.
d) Whether the part is post-yield or just post-buckling it is still a catastrophic failure, except for the rare situation where a snap-through effect is actually desired.
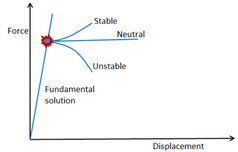
e) Post-buckling you can have stable or unstable buckling and either may take on multiple eventual shapes. See picture below. So what is the point? It has already buckled, therefore failed!
Related myth: Design codes prefer to specify nonlinear buckling.
Reality:
In fact all elastic rules of assessment for steel-framed structures have Euler buckling as part of the Rankine-Gordon equation (see picture below). The other part of the equation just merges this with failure by general plastic collapse which is based on a curve-fit to experimental data. There are other equations available, similar to Rankine-Gordon and none of them are considered as an 'elastic-plastic analysis' or 'nonlinear buckling' just because the yield stress is in the equation: Like many code equations, they are forced fits to real-life tests which have some theoretical underpinnings but also a healthy safety factor added. There is a similar calculation in design codes for other shapes (eg. dished ends) but the safety factors vary, based on comparisons with real-world test results on less-than-perfect shapes.

For FE (often called numerical) analysis assessments an initial stress analysis is a necessary input for the Eigenvalue solution. This of course will be known beforehand and if the membrane stress does not remain elastic then you cannot proceed (by code rules) with a buckling analysis until the part is strengthened. That leaves the S-shaped gray zone where we use calculations rather than a nonlinear analysis. Note that dished heads can also fail at the knuckle under internal pressure and PD5500/EN13445 rules incorporate empirical test data in the thickness calculation for that (for ASME VIII it is a separate calculation). Again, a nonlinear FEA is unreliable for that situation.
For ASME VIII division 2 there are 3 alternative methods of solution for buckling;
1. Euler buckling on the perfect shape with a shape dependent safety factor (typically 2.5).
2. Non-linear buckling on the perfect shape with a slightly smaller shape dependent safety factor (typically 2).
3. Non-linear buckling with shape imperfections included. Partial Safety factors used on loads (typically 2.4).
Method 3 does not mean assume an Euler buckling mode as a guess imperfection (Myth 2): It means you use measured values from a dimensional survey and tweak the model accordingly.
The following paper..
https://asmedigitalcollection.asme.org/PVP/proceedings-abstract/PVP2020/83839/V003T03A022/1089364
Concludes..
"The current design by analysis for protection against collapse from buckling in ASME Section VIII, Division 2, B&PV Code [8] has three different methods. However....analysts have found that the elastic plastic collapse analysis will give overly conservative results when compared with design by rule."
ASME has now introduced a new 5-step plan for shell buckling which seems to be just Method 1 plus a simplistic comparison of membrane stress to yield stress (divided by a safety factor) to cope with potential inelastic yielding.
So 3 conclusions to reach are a) basic theory on perfect geometries needs a safety factor whether elastic or inelastic analyses are used, b) Inelastic analysis can lead you wildly astray, largely due to initial assumptions, and c) comparison with real-life tests by curve-fitting remains the best option, with safety-factored elastic analysis coming second-best. The UK PD5500 code and European EN13445 code (which copied PD5500) had already reached conclusion c) a long time ago though and they still (IMHO) have better design-by-rule buckling methodologies for pressure vessels than the new ASME method.
In summary, nonlinear buckling has niche uses but is not necessary for designing a part to avoid buckling failure! The important thing is ensuring you use the mandated design code safety factors. Don't even bother with buckling analysis unless your part looks slender and is in compression or under external pressure.
*Linear is really a misnomer for Eigenvector analysis. Use Elastic instead.
**At least separate geometric from inelastic nonlinearity.
Lastly don't forget that an iterative solver has not yet been implemented for Femdesigner so you must use the direct solver - which limits the size of models used. If stuck we can let you have Femdesigner Classic for finding the natural frequencies of frames and shells which are the structures most likely to both require modal analysis and run out of memory space if meshed with solid elements.
